Definição e Aplicações

Quando estamos analisando dados para construção de modelos de Machine Learning, alguns dos dados coletados apresentam uma característica especial: a ordem temporal. Essa informação, para o contexto do problema, é bastante relevante, pois a ordem temporal dos dados pode influenciar diretamente no comportamento do modelo.

Para este conjunto de dados, utilizamos o termo série temporal. Uma série temporal é uma sequência de observações coletadas ao longo do tempo. Essas observações podem ser coletadas em intervalos regulares ou irregulares, e podem ser de diferentes tipos, como valores contínuos, categóricos ou binários, por exemplo.

Por que as séries temporais são especiais?

Como mencionado anteriormente, uma série temporal é uma coleção de observações feitas sequencialmente no decorrer do tempo. Ela traz não apenas a informação sobre o valor de cada observação, mas também sobre a ordem em que essas observações foram feitas. Isso faz com que as séries temporais sejam diferentes de outros tipos de dados, como tabelas ou imagens, por exemplo.

Quando analisamos séries temporais, estamos interessados em entender o comportamento dos dados ao longo do tempo, e como esse comportamento pode ser utilizado para fazer predições sobre o futuro. Por isso, é importante que tenhamos em mente que as séries temporais são diferentes de outros tipos de dados, e que a análise desses dados requer métodos e técnicas específicas. Muitas vezes, nossas previsões não estão apenas interessadas em saber o valor futuro de uma variável, mas também em entender como essa variável se comporta ao longo do tempo, indicando padrões e tendências que podem ser úteis para a tomada de decisões.

TLDR - Séries Temporais

Séries Temporais são conjuntos de dados onde a variável independente é o tempo.

Trabalhando com séries temporais

Ao trabalhar com séries temporais, é importante que tenhamos em mente que esses dados possuem uma ordem temporal, e que essa ordem é relevante para a análise. Por isso, é importante que tenhamos em mente que a ordem temporal dos dados deve ser preservada ao longo da análise, e que devemos utilizar métodos e técnicas que levem em consideração essa ordem.

Iniciamos nossa análise da mesma forma que fazemos com outros tipos de dados: coletando, explorando e visualizando os dados. Para isso, vamos utilizar o Python e a biblioteca Pandas, que nos permite trabalhar com séries temporais de forma eficiente e intuitiva. Além do Pandas, vamos utilizar outras bibliotecas para realizar as manipulações dos dados, mas elas serão apresentadas no momento adequado.

Por hora, vamos criar um ambiente virtual e instalar as seguintes bibliotecas nele:

• Jupyterlab
• Pandas
• yFinance

A biblioteca yFinance encapsula e abstrai o acesso aos dados abertos do Yahoo Finance, que é uma excelente fonte de dados para séries temporais financeiras.

Configurando o Ambiente

Vamos criar nosso ambiente virtual e instalar as bibliotecas necessárias. Para isso, abra um terminal e execute os comandos abaixo:

# Windows
python -m venv venv
.\venv\Scripts\activate
# Linux
# python3 -m venv venv
# source venv/bin/activate
pip install jupyterlab pandas yfinance matplotlib

Boa, temos nosso ambiente inicial pronto! Agora, vamos criar um notebook Jupyter e começar a explorar os dados. Pessoal para criar um ambiente com o JupyterLab que não precise de senha, basta rodar o comando abaixo:

jupyter lab --ip='*' --NotebookApp.token='' --NotebookApp.password=''

Obtendo e Explorando os Dados

Agora dentro do nosso notebook:

# Importando as bibliotecas
import pandas as pd
import matplotlib.pyplot as plt
import yfinance as yf

Agora vamos utilizar o yFinance para buscar os dados de uma ação. Isso é realizado informando o código da companhia. Para isso, vamos utilizar o código abaixo:

# Buscando os dados da ação da Apple
apple = yf.Ticker('AAPL')
apple_data = apple.history(period='1y')
apple_data.head()

Se verificarmos o tipo do objeto apple_data, veremos que ele é um DataFrame do Pandas. Isso significa que podemos utilizar todas as funcionalidades do Pandas para manipular e analisar esses dados. Vamos começar explorando os dados obtidos:

print('Tipo dos dados:', type(apple_data))
print('Dimensões dos dados:', apple_data.shape)
print('Colunas dos dados:', apple_data.columns)
print('Informações dos dados:', apple_data.info())

Aqui podemos verificar uma informação importante e relevante para nós: a informação relacionada ao tempo. Para isso, vamos verificar o tipo do índice dos dados:

print('Tipo do índice:', type(apple_data.index))

O índice dos dados é do tipo DatetimeIndex, o que significa que ele é um índice do tipo data e hora. Isso é importante, pois indica que os dados estyão organizados utilizando um índice temporal e que a ordem temporal dos dados é relevante para a análise. Vamos verificar os valores do índice:

print('Valores do índice:', apple_data.index)

Podemos observar que os valores são datas com um intervalo de um dia. Para as análises de séries temporais, o intervalo entre as observações é relevante. Isso indica quais técnicas e métodos podemos utilizar para analisar esses dados. Vamos agora visualizar os dados obtidos:

apple_data.plot(y='Close', title='Preço de Fechamento da Ação da Apple')

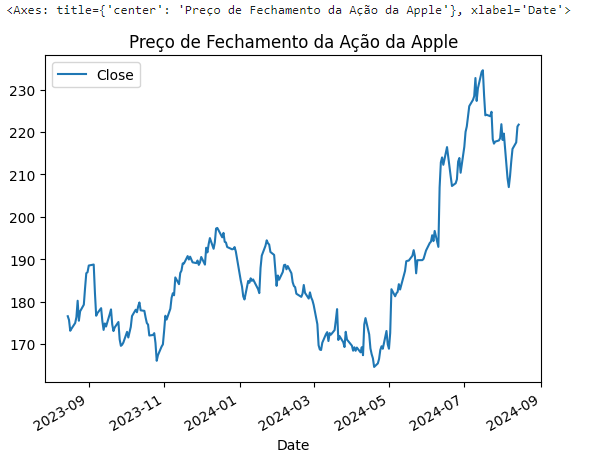
Aqui podemos observar o comportamento do preço de fechamento da ação da Apple ao longo do tempo. Podemos observar que os dados apresentam uma tendência de crescimento, com alguns picos e vales ao longo do tempo. Essa informação é relevante para a análise, pois indica que os dados apresentam um comportamento específico que pode ser utilizado para fazer previsões sobre o futuro. Vamos avaliar agora algumas características e termos utilizados com frequência em séries temporais.

Vocabulário de Séries Temporais

As séries temporais podem ser:

• Univariadas: quando possuem apenas uma variável dependente;
• Multivariadas: quando possuem mais de uma variável dependente.

Elas também pode apresentar como característica:

• Discreta: quando as observações são feitas em intervalos regulares;
• Contínua: quando as observações são feitas em intervalos contínuos.

Além disso, as séries temporais podem ser descritas por 4 componentes principais:

• Sazonalidade: padrões que se repetem em intervalos regulares. Esses intervalos podem ser diários, semanais, mensais, anuais, por exemplo;
• Tendência: padrões de crescimento ou decrescimento ao longo do tempo;
• Ciclos: padrões que se repetem em intervalos não regulares, são semelhantes à sazonalidade, mas não possuem um intervalo fixo;
• Ruído ou Fator Aleatório: variações aleatórias nos dados.

As séries podem ser decompostas de duas maneiras:

• Aditiva: quando a série é a soma das componentes;

  $$Y(t) = T(t) + S(t) + R(t)$$

• Multiplicativa: quando a série é o produto das componentes.

  $$Y(t) = T(t) \times S(t) \times R(t)$$

Uma outra característica importante quanto as séries temporais é a estacionariedade. Uma série é considerada estacionária quando suas propriedades estatísticas, como média e variância, são constantes ao longo do tempo. Isso é importante, pois muitos dos métodos e técnicas utilizados em séries temporais assumem que os dados são estacionários.

Continuando a Análise

A decomposição de uma série temporal envolve a separação da série em seus componentes fundamentais, geralmente em tendência, sazonalidade, e resíduo (ou ruído). Este processo ajuda a entender melhor o comportamento da série e é útil para análise e modelagem. Existem diferentes métodos para decomposição, mas os dois mais comuns são a decomposição aditiva e a decomposição multiplicativa.

Primeiro vamos precisar instalar a biblioteca statsmodels:

pip install statsmodels

Agora vamos importar a biblioteca e realizar a decomposição da série temporal:

from statsmodels.tsa.seasonal import seasonal_decompose

# Decompondo a série temporal
decomposition = seasonal_decompose(apple_data['Close'], model='multiplicative', period=30)

# Plotando a decomposição
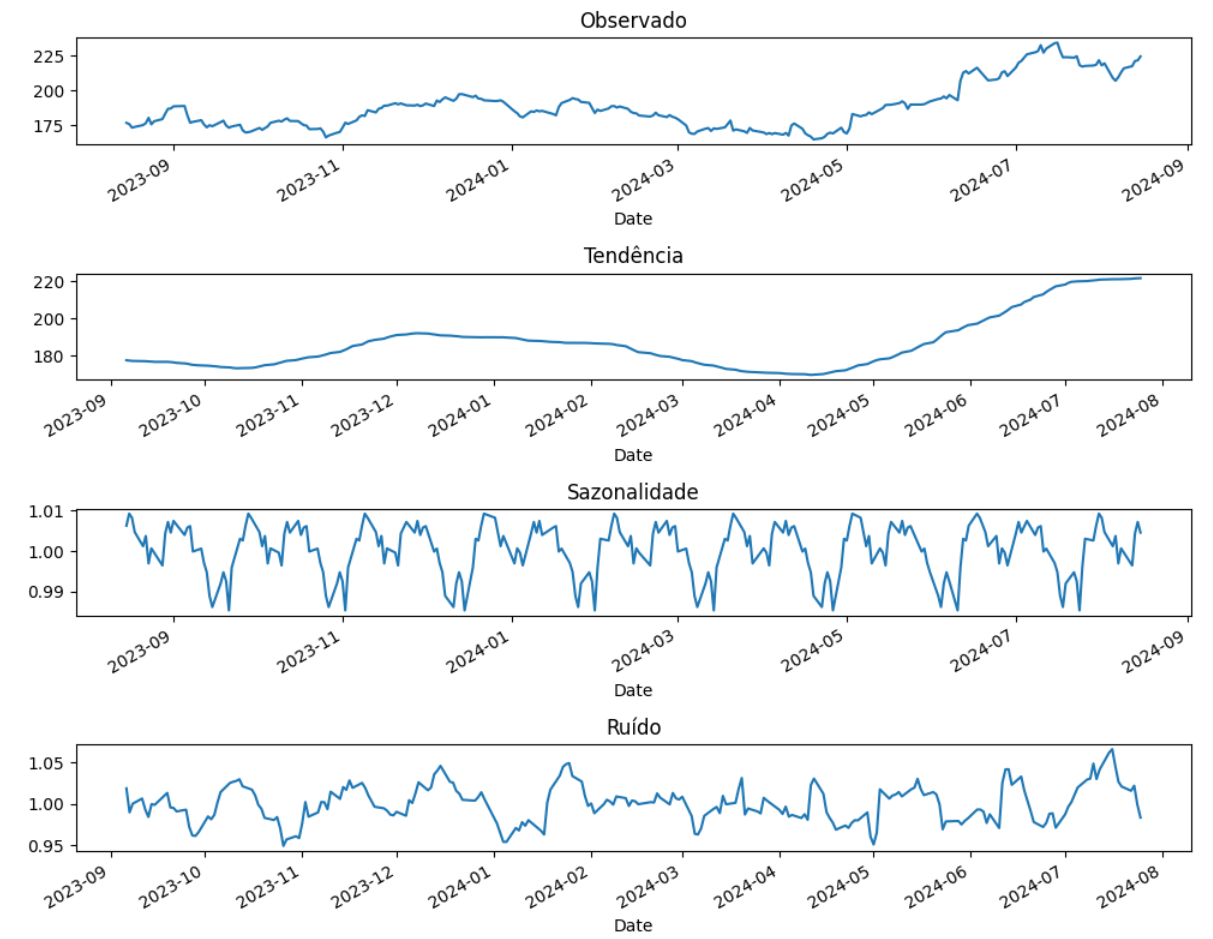
fig, axes = plt.subplots(4, 1, figsize=(10, 8))
decomposition.observed.plot(ax=axes[0], title='Observado')
decomposition.trend.plot(ax=axes[1], title='Tendência')
decomposition.seasonal.plot(ax=axes[2], title='Sazonalidade')
decomposition.resid.plot(ax=axes[3], title='Ruído')
plt.tight_layout()

• Observado (observed): Mostra a série original.
• Tendência (trend): Mostra a direção geral da série ao longo do tempo.
• Sazonalidade (seasonal): Mostra os padrões repetitivos que ocorrem em intervalos regulares.
• Resíduo (resid): Representa as flutuações aleatórias não explicadas pela tendência ou sazonalidade. Se o modelo for bom, o resíduo deve parecer um ruído branco, sem padrões óbvios.

Criando um Modelo de Previsão - ARIMA

Agora que já exploramos e entendemos melhor os dados, podemos começar a criar um modelo de previsão. Para isso, vamos utilizar o modelo ARIMA (AutoRegressive Integrated Moving Average), que é um dos modelos mais utilizados para previsão de séries temporais. O modelo ARIMA é composto por três componentes principais:

• AR (AutoRegressive): Modelo autorregressivo, que utiliza os valores passados da série para prever o valor futuro.
• I (Integrated): Modelo integrado, que utiliza a diferença entre os valores da série para tornar a série estacionária.
• MA (Moving Average): Modelo de média móvel, que utiliza os erros passados da série para prever o valor futuro.

Para iniciar a construção do modelo, vamos utilizar o pacote AutoARIMA da biblioteca pmdarima. Para instalar a biblioteca, execute o comando abaixo:

pip install pmdarima

Agora vamos importar a biblioteca e criar o modelo ARIMA. Importante ressaltar que o modelo ARIMA é um modelo estatístico e, por isso, é importante que os dados sejam estacionários. Caso contrário, é necessário realizar a diferenciação dos dados para torná-los estacionários.

Para verificar se os dados são estacionários, podemos utilizar o teste de Dickey-Fuller, que é um teste estatístico utilizado para verificar a estacionariedade de uma série temporal. Para isso, vamos utilizar a função adfuller do pacote statsmodels:

from statsmodels.tsa.stattools import adfuller

# Teste de Dickey-Fuller
result = adfuller(apple_data['Close'])
print('Estatística do teste:', result[0])
print('Valor-p:', result[1])
print('Valores críticos:', result[4])

Como podemos interpretar o resultado do teste de Dickey-Fuller?

• Se a estatística do teste for menor que o valor crítico, rejeitamos a hipótese nula e a série é estacionária.
• Se o valor-p for menor que 0.05, rejeitamos a hipótese nula e a série é estacionária.

Os valores críticos são os valores que a estatística do teste deve ser menor para rejeitarmos a hipótese nula. Se a estatística do teste for menor que esses valores, rejeitamos a hipótese nula e a série é estacionária. Caso contrário, não podemos rejeitar a hipótese nula e a série não é estacionária.

TLDR - Teste de Dickey-Fuller

O teste de Dickey-Fuller é um teste estatístico utilizado para verificar a estacionariedade de uma série temporal. Se a estatística do teste for menor que o valor crítico e o valor-p for menor que 0.05, a série é estacionária. ELe foi criado por David Dickey e Wayne Fuller em 1979. Para saber mais, acesse este link.

Caso os dados não sejam estacionários, podemos realizar a diferenciação dos dados para torná-los estacionários. Para isso, podemos utilizar a função diff do Pandas:

# Diferenciando os dados
apple_data['Close_diff'] = apple_data['Close'].diff()
apple_data['Close_diff'].plot(title='Diferença dos Dados')

Agora para aplicar o teste novamente:

# Teste de Dickey-Fuller
result = adfuller(apple_data['Close_diff'].dropna())
print('Estatística do teste:', result[0])
print('Valor-p:', result[1])
print('Valores críticos:', result[4])

O dropna() é utilizado para remover os valores nulos gerados pela diferenciação dos dados. Agora que os dados são estacionários, podemos criar o modelo ARIMA. Vamos primeiro criar um modelo com a função auto_arima?